特集! 軟X線、高次高調波向け回折格子 ユーザーインタビュー記事 はこちら
1-1. 回折とは?
回折格子(Gratings:グレーティング)は、種々の波長が混ざった光(白色光)を波長ごとにわける(分散)光学素子です。最も単純な回折格子は、多数の平行スリットが等間隔で配列した構造をしています。白色光が回折格子に入射すると、波長ごとに決まったある角度で光が強め合い(回折)、この強め合った光を取り出すことで波長選択ができます。すなわち、図1のように隣り合う開口に入射した平行光線について、その光路差が波長の整数倍になるとき光は強め合います。同様に、すべての開口からの光もこの方向に強め合い、この強め合った光を回折光と呼びます。
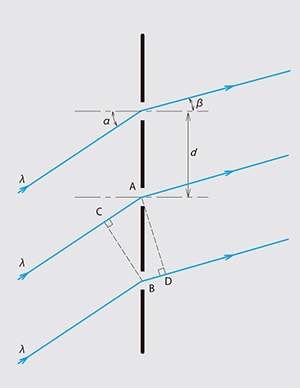
図1-1 回折格子の原理( 透過型)
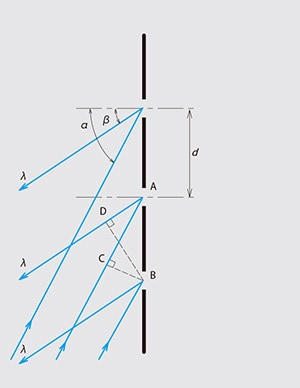
図1-2 回折格子の原理( 反射型)
1-2. 回折格子方程式
図1-1, 図1-2 のように、入射光と回折格子法線とのなす角(入射角)をα 、回折光と回折格子法線とのなす角(回折角)をβ とすると、以下のような関係式が成り立ちます。図1-1のような透過型の場合は光路差がCA-BD となり、
![]() (1)
(1)
あるいは、
![]() (2)
(2)
同様に図1-2 のような反射型の場合は、光路差が CA + ADとなり、
![]() (1)'
(1)'
あるいは、
![]() (2)'
(2)'
- d : 開口の間隔(回折格子周期)
- N : 1mm あたりのスリット数(溝本数)
(回折格子周期の逆数) - m : 回折次数(m=0,±1,±2,・・・)
- λ : 波長
この関係式により、m = 0 のときの光(0 次光)はすべての波長で直進するため、0次光では波長分離ができないことがわかります。またm ≠ 0 のときは、波長ごとに回折角β が異なることがわかります。これが白色光を回折格子により波長分離できる理由です。また回折角β は、溝本数N と入射角αによっても変わることがわかります。ここで注意することは、溝本数N により回折光を得られない場合があるということです。たとえば、透過型回折格子において入射角α = 30°、溝本数N = 2400 本/mm の回折格子のm =+ 1 の光(+ 1 次光)の場合,波長λ = 700nm ではsinβ = 1.18 となり、回折光が得られません。
1-3. 波長分解の指標
異なった波長が回折格子(Gratings:グレーティング)に入射したとき、回折角βがどのくらい変化するかということは、波長の分離を考えるときに重要な要因になってきます。入射角αを一定として(2)式の両辺をλで微分すると、
![]() (3)
(3)
となります。ここでdβ/dλ は角分散と呼ばれる値で、これにより波長変化dλ に対する回折角度変化dβ を求めることができます。
(3)式の両辺に光学系の焦点距離f をかけると、
![]() (4)
(4)
となります。f ・dβ=dxとし、両辺の逆数をとると、
![]() (5)
(5)
となります。このD は逆線分散と呼ばれ、光学系の出口スリット面上での単位長さあたりの波長差を意味します。このD にスリット幅を掛けると、波長分解の指標となります。




