特集! 軟X線、高次高調波向け回折格子 ユーザーインタビュー記事 はこちら
5-1. トロイダル回折格子
トロイダル回折格子は凹面回折格子に分類される回折格子で、トロイダル面の形状は直交する中心軸の二つの曲率半径で表されます。横方向の曲率半径をRh、縦方向の曲率半径をRvとすると、トロイダル面の形状は、以下のような関係式が成り立ちます。
![]() (16)
(16)
等間隔直線溝トロイダル回折格子の近軸焦点位置は(17)式、(18)式で表すことができます。r は入射距離、r'hは横方向焦点距離、r'v は縦方向焦点距離、α、β は回折格子方程式(2)'を満たすものとします。
![]() (17)
(17)
![]() (18)
(18)
図のような球面基板(Rh=Rv)ではr'h、r'v の焦点距離が異なるため非点収差が生じますが、トロイダル基板(Rh≠Rv)を用いて適切に設計することによりr'h≒r'v となり非点収差を補正することができます。
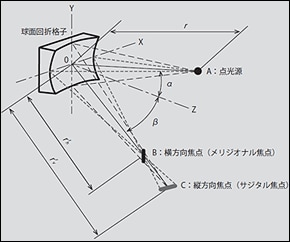
球面回折格子の異なる焦点
5-2. 収差補正型フラットフィールドポリクロメータ用凹面回折格子
光学配置
ポリクロメータは、回折格子を回転させずに各波長のスペ クトル分布をフォトダイオードアレイ等の検出器を用いて、同時測光できる分光器です。図のように入口スリットA から出た光は凹面回折格子によって分光され、そのスペクトルが検出器面上(B1~B2)で測定されます。スペクトル面は可能な限りフラットに設計されており、コマ収差、非点収差等の極小化にも注意が払われています。 波長λのときの回折角β、および回折格子中心Oから検出器面までの距離r'は(22) 式、(23)式となります。
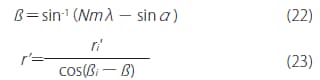
また、ポリクロメータの場合は(5)式の逆線分散が(24)式となります。
![]()
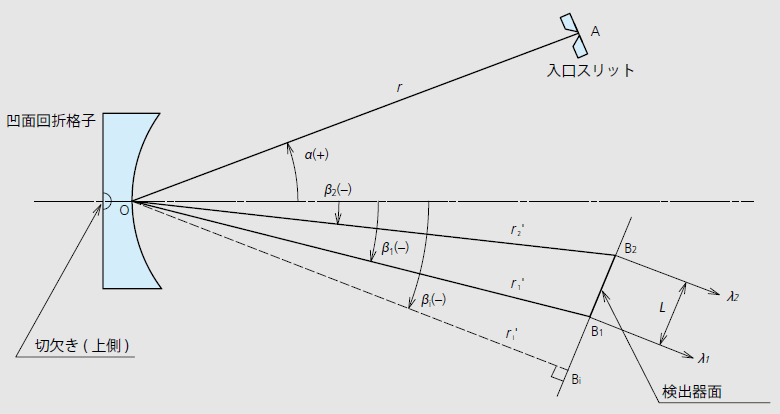
フラットフィールド ポリクロメータ用凹面回折格子マウント
5-3. 収差補正型定偏角モノクロメータ用凹面回折格子
光学配置
定偏角モノクロメータとは、入口スリットと出口スリットを固定し、回折格子の回転のみで波長走査を行えるコンパクトな分光器です。一般に、入射光と回折光とのなす角を偏角と呼び、図のように回折格子中心、入口スリット、出口スリットをそれぞれO 、A 、B とすると、∠AOBが一定角となり、2K で表わします。回折格子の回転角をθとすると、入射角α 、回折角βと2Kとの関係は、2K =α-β =const.、α =K +θ、β =θ-Kとなります。ただし、α 、β 、θは回折格子法線からの角度で反時計回りを正とします。すると回折格子方程式(8)式は。
![]()
となります。この式より回折格子の回転角θのみで波長走査を行えることがわかります。
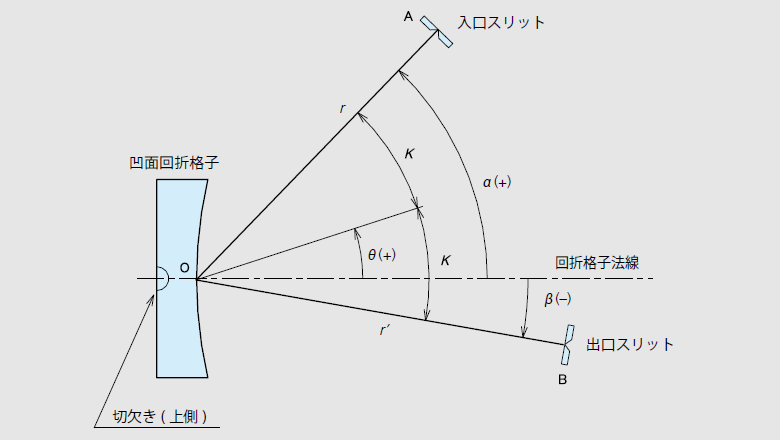
定偏角モノクロメータ用凹面回折格子マウント




